Boundary Dimensions

Description

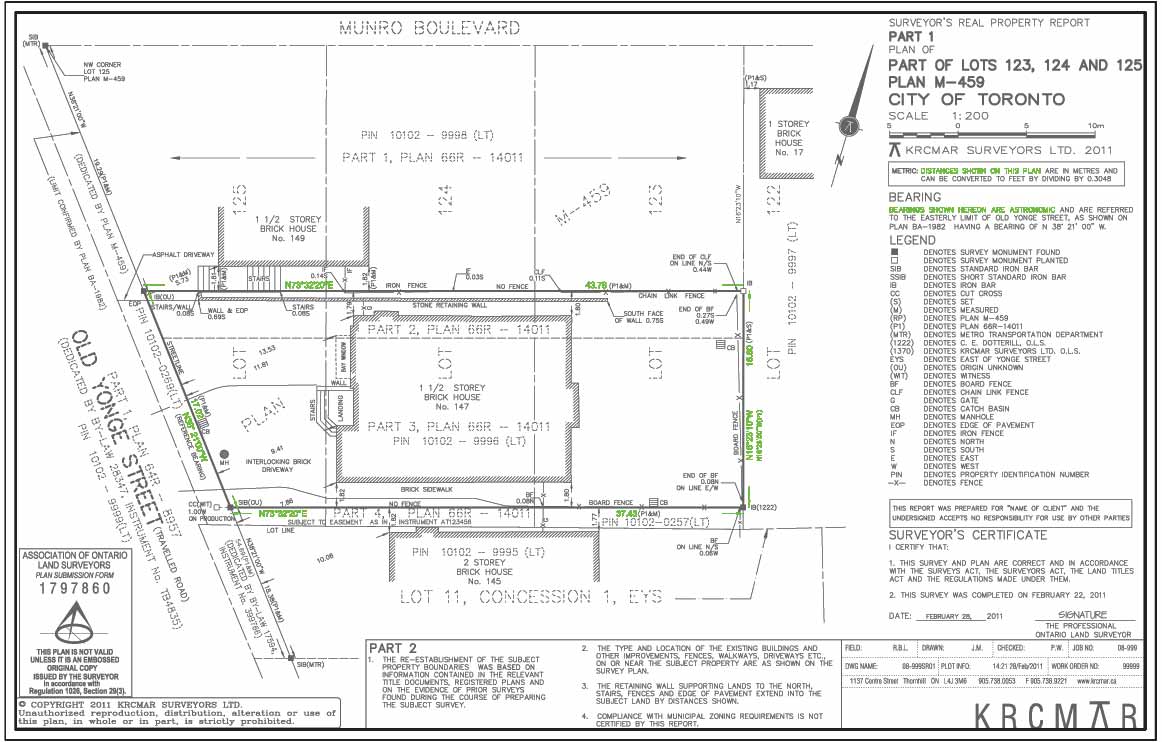
Boundary dimensions are comprised of both exact distances and compass directions (known as bearings). Both are needed to mathematically describe each line along the perimeter of the property. On this survey the property appears rectangular (or as a parallelogram) but is really a four sided trapezoid because the side lines are not parallel nor the front and back distances equivalent. Both bearings and distances are needed for each line shown on any polygon shaped property that can be mapped on a survey plan. (for further explanation see below*). Some boundaries are curved but are still dimensioned with the radius, chord and arc length described. All lines have two components that are shown on a plan, namely: Distances Everyone has measured distances. Whether preparing a dress pattern or doing carpentry the consequences of improper distances are readily appreciated. Boundary distances must also be exact and are measured by surveyors using precisely calibrated equipment. Older means of measuring using tapes and chains are often less exact as are the distances called for in deed documents. Comparisons with these older measurements are often shown on plans as required by Generally Accepted Surveying Principles. Some boundaries are curved. These are additionally described with the addtion of the radius (R=), the arc length (A=) and the chord length (C=). Bearings Bearings are angular measurements exactly like those made using a protractor in geometry class. The orientation used is relative to north and are based on divisions of a 360 degree circle. Surveyors use them much the same someone would use a handheld compass except we do not refer to the southerly direction on our plans. We relate all bearings only to the northwest or north east quadrants shown on the face of a compass. Each degree is broken into 60 minutes which in turn are comprised of 60 seconds. Surveyor's instruments (theodolites, transits and total stations) actually measure to this degree of accuracy. The difference that one second of angular measure for a distance between Toronto and Hamilton is about one foot. Dimension Arrows These are graphic aids that help the reader determine exactly where the dimensions are being measured on the plan. In this case they are shown to the corners of the property * Every Point on a graph can be described either as a coordinate (x,y) position or as the end of a vector,(angle and distance) from a point of origin. This is also true of mapped positions on the face of the earth. The boundary component of a survey plan is actually a mathematical model of the property describing the exact size and shape of the parcel presented in angle and distance format. Many plans that are currently prepared also show coordinates of key corners. From these the parcel's unique location on the earth's surface can be demonstrated. with an exact orientation.

Purpose

Each dark and bold boundary line is expressed by dimensions (distances and bearings/directions).

Why is this important?

This provides key measurements of the property - the dimensions of the perimeter boundary.